A NEW VERSION HERE!

A few people have provided some feedback on this version. I wanted to play around with python and there were a few things I didn't like about this version of the so... Why not completely rebuild it? The updated guide is available here: https://www.dr-b.io/post/Duet-3D-Printer-TimeLapse-V2

I will keep an eye on comments/feedback from this version but please try the new version - I think it will be easier to implement and more reliable than this version.

The problem:

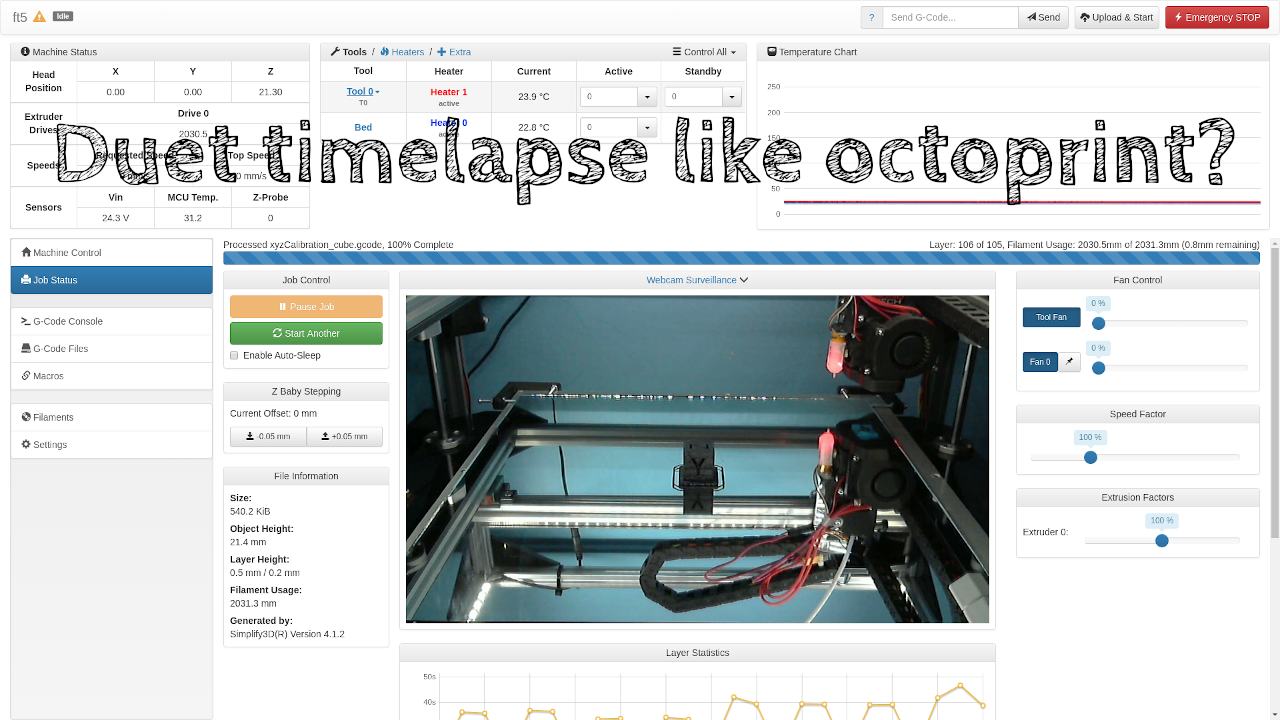
I have been playing with 3D printers for a few years now. The ability to design something and quickly (relatively speaking) print out a functional prototype is very intriguing. My first couple of printers were tethered to a computer of some sort with a USB cable, and I eventually started using OctoPrint installed on a Raspberry Pi. OctoPrint provided a beautiful web GUI to control the printer and could create time-lapse videos. I eventually upgraded my last printer to a Duet WiFi controller. As lovely as it is and as much as I love it (there are a few drawbacks, but I will not get into them here), I really missed the ability to create those time-lapse videos easily. 

I did a little research and figured out that the Duet webserver can be sent some specific queries to get the printer status (file name of the print job, x/y/z coordinates of the print head, etc.) and I thought I could use that as a starting point for my own time-lapse creation. The short video below is created by this process with a Raspberry Pi, both hosting the mjpeg stream that is used to grab the images and the processes to take the completed still images into a time-lapse video. While this video is just a small calibration cube, it does show the process in action. Larger prints are much more exciting to watch in a timelapse, but this gets the point across.

The solution:

The solution to this particular issue only took me a bit of time. Since I had already used OctoPrint (and if you still have your printer tethered with a USB cable, I HIGHLY recommend OctoPrint) I had a webcam and Raspberry Pi. If you don't already have those, you can get them both from Amazon for less than $100: Raspberry Pi and  Logitech Webcam (this is not the same webcam I am using but it *should* work). The Pi in this link is an older Pi 3, the newer Pi 4 would be faster creating the video, but I have never had any issues with the older Pi 3 I am using.

I uploaded the script to GitHub, if you are comfortable pulling a repo you can get it here: https://github.com/dr-b-io/dmc but if you want a little help walking through the process just follow along!

First things first:

These directions DO NOT step you through setting up the video source. You can use any mjpeg stream source for the still images that will be captured by this process. I personally am using mjpg_streamer, and there are many guides on the interwebs that explain how to get it up and running. I honestly do not remember what guide I used, but the following seems to be recent and is pretty straight forward: https://github.com/cncjs/cncjs/wiki/Setup-Guide:-Raspberry-Pi-%7C-MJPEG-Streamer-Install-&-Setup-&-FFMpeg-Recording. You only really need the first block to get mjpg_streamer running but the autostart script may be useful, I have not tried it. You do not HAVE to use a Pi and Webcam as the image source - you can use ANY mjpeg source. I have tested with a cheap IP based reolink security camera and it worked without complaints. YMMV.

Get the code:

With that out of the way, let's get started! Open a terminal and make sure you have the pre-requisites installed:

sudo apt update && sudo apt install curl jq ffmpeg git -y

Now let's download the needed files from GitHub:

cd ~
git clone https://github.com/dr-b-io/dmc.git

You should now have a folder called dmc in your home directory, move into it, and rename a configuration file:

cd dmc
cp DuetMonitorCapture.config.dist DuetMonitorCapture.config

Two changes need to be made in the configuration file:

nano DuetMonitorCapture.config

Find these two lines and update them for your system:
PRINTER=URL_TO_DUET - this should be updated to the name or IP address of your Duet (http://printer.local as an example)
MJPEG_SOURCE - this should be the full URL to your mjpeg source (http://192.168.1.10:8080/?action=snapshot as an example)
Save and close the file (CTRL+X -> Y -> Enter)

Now you are ready to test the process!

. DuetMonitorCapture.shl

You should see a few lines of output where the process starts, then every few seconds you should see another line where the process checks the z-height of the printer and the printer status. This would be a good time to start a small print and let the process grab some snapshots (one at each z-height) and create the video. You may see some complaints when ffmpeg is running, but I have not had any issues with the video that is output. When the process is done, it will remove all of the jpeg still images that were created, and you will have a video named after the file you just printed in the snapshots directory that was just created. 

Please note this comment from one of our users. We have not been able to replicate this issue but it should be kept in mind: This works great, however with the latest Duet 2 Wifi and latest RepRap Firmware, The DuetMonitorCapture.shl script needs to be changed up a bit. When it pulls the $File value, it also pulls the folder path from the Duet. looks something like this: "snapshots/0:/duet/FileName/ To resolve this I removed the $File from the file paths of the save locations. When we are able to replicate the issue we will update the git repository with a resolution.

Do I have to remember to start this process at the beginning of each print?

Absolutely not! You can run the following command whenever you boot/reboot your system (Raspberry Pi in my case), or you can add it to a startup script. Nohup tells the system to keep the process running when the terminal closes (No Hang Up) and the ampersand tells the process to return to a prompt immediately.

nohup sh ~/dmc/DuetMonitorCapture.shl&

The process will monitor the Duet and start taking still images whenever it sees the status change to printing. When the printer goes back to idle it will compile the stills into a video and save it with the prints file name. If you print the same item multiple times, it will try to overwrite the video each time - if you want to keep them, you should copy them before you start the next print. 

When you get done with a print, copy the compiled video and post it wherever you want. Simple as that!

Items used in this guide:

• Duet 2 Wifi - Duet 2 printer controller board
• Folger Tech FT-5 - My most recent printer, with a few DIY upgrades this thing is a beast!
• Raspberry Pi - but any Debian based computer should work
• Logitech Webcam - connected to my Pi but any mjpeg source will work
• https://www.sigmdel.ca/michel/ha/rpi/streaming_en.html - mjpeg_streamer setup resource
• https://github.com/cncjs/cncjs/wiki/Setup-Guide:-Raspberry-Pi-%7C-MJPEG-Streamer-Install-&-Setup-&-FFMpeg-Recording - better mjpg_streamer resource, you just need the first block to build/install mjpg_streamer
  
• GitHub - GitHub, the place for many great projects!
• OctoPrint - I'm not using it anymore but if you have your printer controlled by USB you should really check it out. Great project with a great community behind it!